In Emolecipation, talking moles have built what appear to be islands, but are actually rafts born up by countless bobblenuts. (like a coconut, but twice the size)
Their shells are extremely strong and durable, and when treated with certain oils, can last centuries in seawater without cracking or eroding. (a big claim, I know. I might be handwaving this part a smidge)
Even regular coconuts can form rafts. But how many bobblenuts would it take to bear up a small island? Here are a list of assumptions (approximate figures used):
- The island is 0.5 miles on a side, or 0.25 square miles
- The soil of the island weighs 75lbs per cubic foot
- The soil layer is 12ft high between the top of the bobblenut raft to the surface (this gives plenty of depth for roots for the many species of trees that would grow here)
- Each bobblenut displaces 1 gallon of seawater
- 1 gallon of seawater weighs 8.6lbs
- There are 2,640 feet in a half-mile
- Soil volume is 2,640ft x 2,640ft x 12ft = 316,831,680 cubit feet
- That volume of soil weighs 23,762,376,000 lbs (316,831,680 cu ft x 75lbs/cu ft)
So, to bear up 23,762,376,000 lbs of soil, there must be enough volume of bobblenuts to displace that same weight of seawater (Archimedes principle: https://en.wikipedia.org/wiki/Archimedes%27_principle) Put another way, the entire raft must weigh < the volume of water the raft displaces. For a simple example, 1 bobblenut that takes up 1 gallon of space can support up to 8.6lbs of load. Actually a little less when you add the weight of the bobblenut shell itself. Now for the scaled up numbers:
- Seawater weighs 64lbs per cubic foot https://www.tripsavvy.com/buoyancy-salt-water-vs-fresh-water-2962936
- 316,831,680 cu ft of seawater weighs 20,277,227,520 lbs (316,831,680 cu ft * 64 lbs/cu ft)
- 20,277,227,520 lbs / 8.6lbs = 2,357,817,153.5 bobblenuts! (round up to 2,357,817,154)
How much volume would 2,357,817,154 bobblenuts occupy under the soil?
- 1 gallon = 0.134 cubic feet
- Island area is 2,640ft x 2,640ft = 6,969,600 sqft
- A bobblenut of 7.6128 square inches will hold 1 gallon of water (bobblenuts are not square, but we assume they effectively occupy a full square of space. Of course, this need not be true if they’re packed efficiently, but we assume they aren’t for ease of calculation)
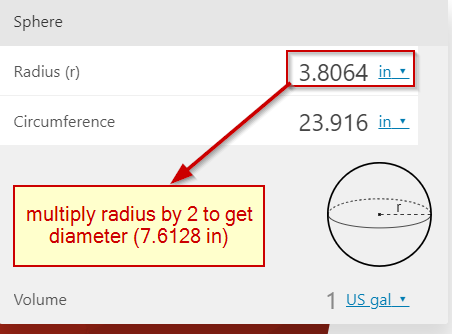
- 2,640ft = 31,680 inches on a side (2,640ft x 12in/ft)
- 31,680in/7.6128in = 4,161.412 bobblenuts across a side (round up to 4,162)
- 4,162 x 4,162 = 17,322,244 bobblenuts (this is how many each layer will hold)
- 2,357,817,154/17,322,244 = 137 layers of bobblenuts needed
How tall would 137 layers of bobblenuts be? (this would likely all be underwater)
- A bobblenut is 7.6128 inches tall
- 137 layers x 7.6128in/layer = 1,042.95in (or 86.91ft)
Now, the island is made of more than just soil. It would also have bobblenut trees and other vegetation, watering holes, rocks and shells, small animal life, and rainwater that collects in the soil after each storm. Not to mention the weight of the bobblenut shells themselves and the lashings that bind them together. So to account for all that extra weight, there might be 3 more layers of bobblenuts. The foundation would then be 140 bobblenuts high and 88.816 feet tall. Here’s a sketch:
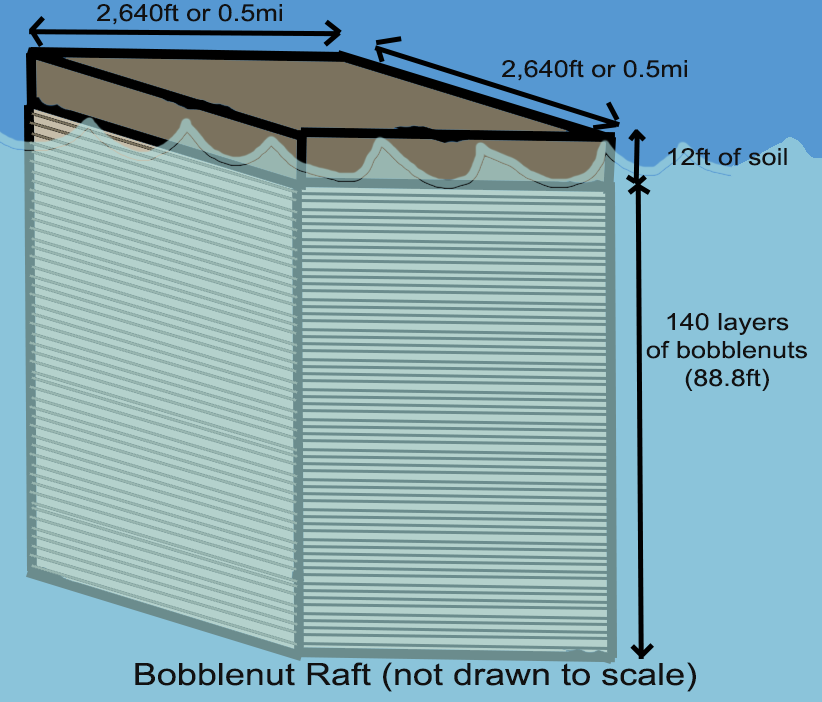
Also, long tree trunks in the bobblenut foundation would jut down from the bottom to give the whales something to push against so they can propel the island:
These trunks would need to be around 100 feet long and made of wood that’s strong enough to withstand lateral forces without snapping. These poles don’t allow the whales to exert downward force, which could drag the whole raft underwater.
Can whales tug such a heavy structure? I think so. Consider how a tiny boat tugs an aircraft carrier:

How much force would the pod of whales need to impart on the island to tug it? More rough math:
- The island weighs > 23,762,376,000 lbs (just the soil weight) or 11,881,188 tons.
- An aircraft carrier weighs 90,000 tons or 180,000,000lbs.
- The island would weigh as much as 132 aircraft carriers
- Blue whales (on Earth) can generate 600 horsepower (https://a-z-animals.com/blog/the-10-strongest-animals-on-earth/)
- A navy tugboat that pulls aircraft carriers generates 2,000 shaft horsepower (and I’m betting they don’t use all 2,000 SHP to do so) (https://www.dvidshub.net/news/160191/tugboats-gtmo)
- Therefore, on the basis of horsepower, it would take about 4 Earth-like blue whales to tug an aircraft carrier. Multiply that by 132 and you get 528 blue whales needed to tug an island this size.
There is a more rigorous way to calculate the needed force, but it involves using a bollard pull calculator, which is pretty complicated. (https://www.mermaid-consultants.com/bollard-pull-calculation-of-ship.html)
Can 528 blue whales really fit under an island this size? I believe so, but I don’t know it would really take that many. After all, nothing stops me, the all-powerful worldbuilder, from creating whales that are much stronger than the blue whales of earth. Mwa ha ha! If the whales on Daishon are four times stronger than blue whales on Earth, then it would take about 132 of them to tug one island of this size. That number could definitely fit under the island.
“The typical Blue Whale has an overall height of 13’-16’… and body length of 82’-105’ ” https://www.dimensions.com/element/blue-whale-balaenoptera-musculus
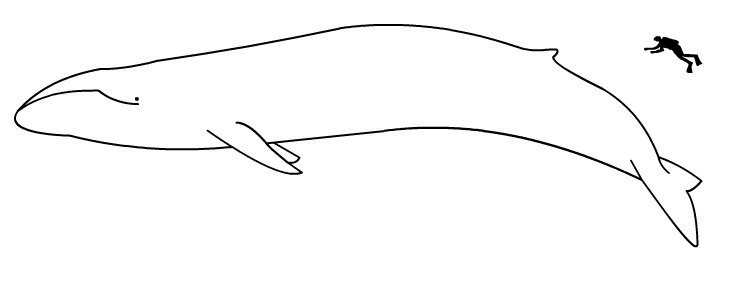
From the height of 15 feet, the tree trunk poles the whales push against needn’t protrude from the bottom of the island by more than maybe 20 feet. And if those poles are laid out in a grid pattern across the bottom of the bobblenut foundation, there is plenty of room between poles to fit hundreds of these whales. 2,640ft/100ft = 26.4 (or around 26 whales on a side). 26 x 26 = 676 whales can fit.
Now, how much plankton and small fish would there need to be under the island to feed all these whales? Well, I could break out all the math for that, but I’m mathed out about now. I’m guessing you are, too. Let’s just say that based on my napkin figures, it looks like such a structure is at least moderately plausible. Of course this assumes the shells of each shell is strong enough to withstand the weight of the column of soil above it.
Okay, I lied about being done with math. Here’s some more:
- The column of soil would be 12ft tall by 7.6128 in wide by 7.6128 in long
- Total volume is 4.829 cubic feet
- 75lbs/cu ft * 4.829 cu ft = 362.175lbs of total load (assuming no tree rests on that spot)
Could a bobblenut hold 362lbs? According to these videos, aged coconuts on Earth can hold up somewhere between 200lbs and 941lbs: https://www.youtube.com/watch?v=UkXHZkJNgGo (220lbs) and https://www.youtube.com/shorts/jQjoegmJ9b4 (427kg or 941lbs)
So is it reasonable for bobblenuts to support the weight of the island? I think so, especially if I decided that bobblenuts have a higher cellulose percentage than coconuts and have thicker shells, both of which would make them stronger.
Aside from weight and towing, there are many other design considerations. How well would it hold up under various categories of hurricanes? What shape should it be to prevent tipping? Would it have enough soil and organic matter to prevent runoff? Just how fast could whales pull this structure? How would the bobblenuts be held together? I might try addressing those subjects in another newsletter, but for now, all those numbers have made my head hurt. I’m going to get some ice cream therapy.
Anyone want to try building one of these island rafts out of coconuts? Reply and share photos of your creation 🙂
See you next month!
Dylan West

Wow the maths involved in this blew my mind, and I love numbers!
It takes some imagination to toy with such an idea let alone turn it into a book.
Having read the first chapter of said book. I am intrigued to read more.
I have only just found your work and I feel I want more.
Nice post.
This is an interesting post! I was wondering, what kind of oils are used to treat the bobblenuts so that they can last centuries in seawater without cracking or eroding?
Thanks, Zoe! Great question, and I haven’t taken time to think about that yet 🙁 I probably will before I write the next episode of Emolecipation, though.